Fast and Uncertainty-Aware SVBRDF Recovery from Multi-View Capture using Frequency Domain Analysis

Anonymous authors,
ArXiv 2024
Paper (ArXiv PDF) Supplementary Code (to be released) arXiv
Overview image.

We present fast and uncertainty-aware multi-view material acquisition for objects captured in uncontrolled setups. We propose to build upon and extend the signal processing framework for inverse rendering by Ramamoorthi and Hanrahan (2001): we improve the model with shadowing and masking and propose a lightweight objective function for BRDF fitting using spherical harmonics power spectra (center). We then use this approximation to provide a measure of uncertainty relying on statistical entropy. We show that our material estimation is significantly faster than previous work and achieves similar or better results (right).

Abstract

Relightable object acquisition is a key challenge in simplifying digital asset creation. Complete reconstruction of an object typically requires capturing hundreds to thousands of photographs under controlled illumination, with specialized equipment. The recent progress in differentiable rendering improved the quality and accessibility of inverse rendering optimization. Nevertheless, under uncontrolled illumination and unstructured viewpoints, there is no guarantee that the observations contain enough information to reconstruct the appearance properties of the captured object.

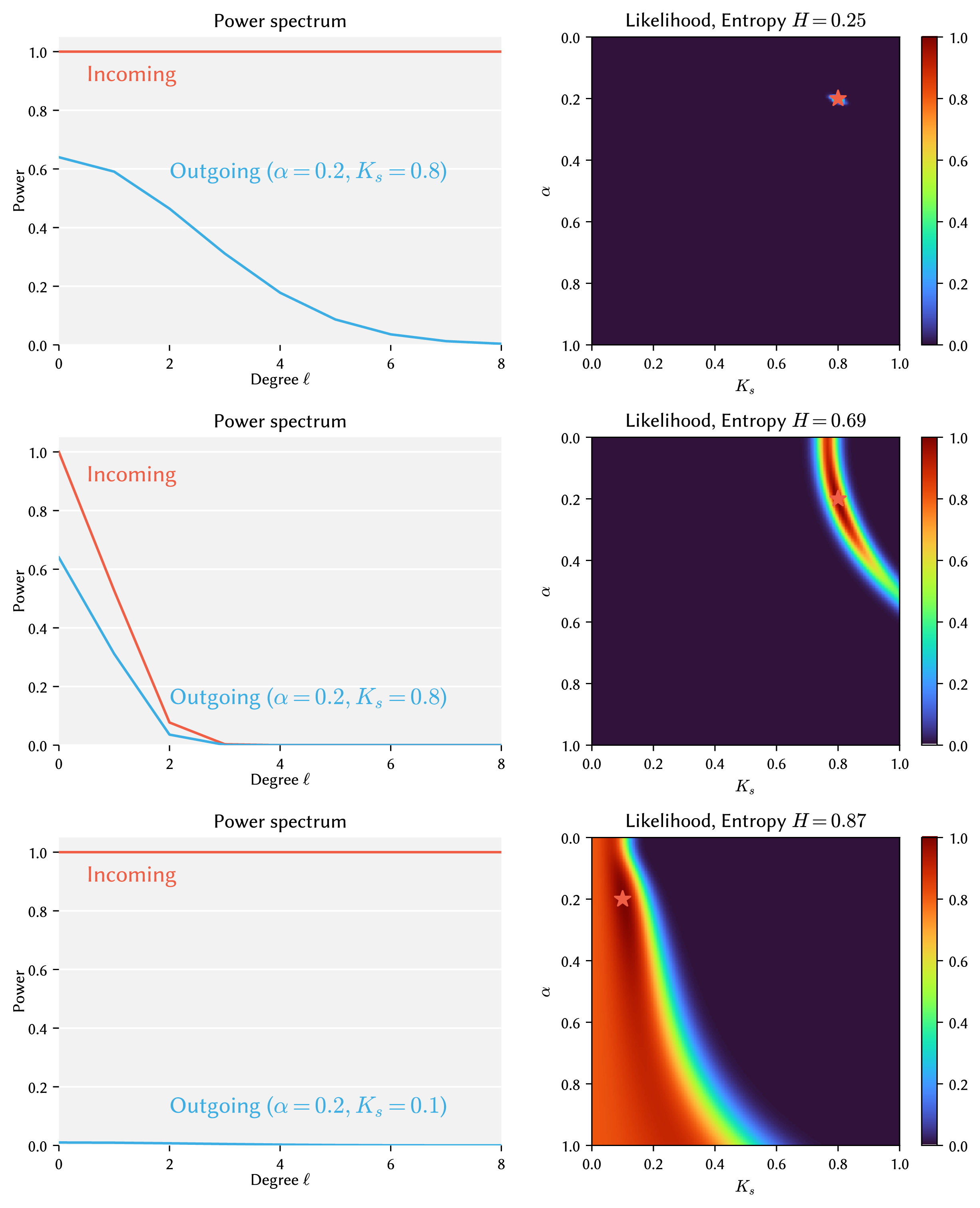
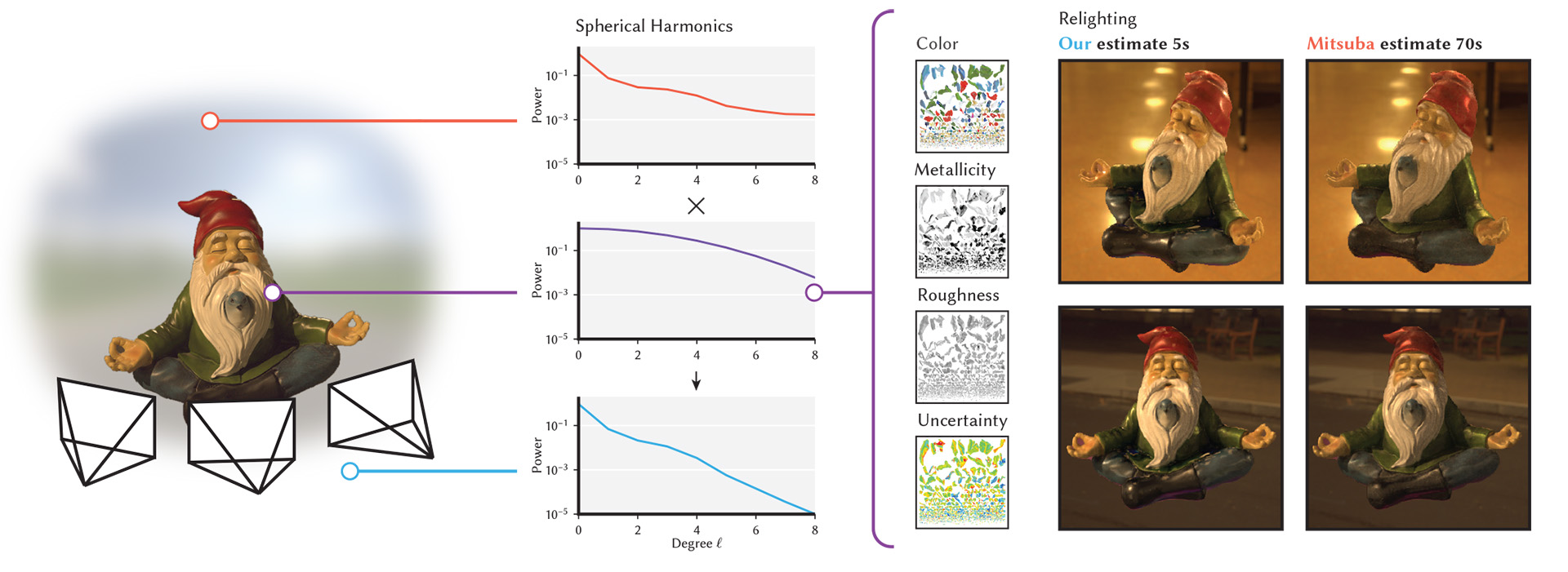
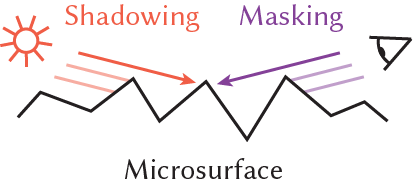
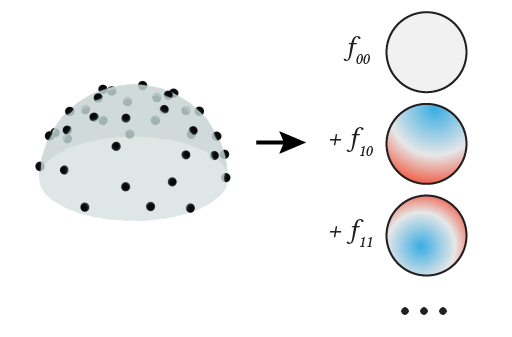
We thus propose to consider the acquisition process from a signal-processing perspective. Given an object's geometry and a lighting environment, we estimate the properties of the materials on the object's surface in seconds. We do so by leveraging frequency domain analysis, considering the recovery of material properties as a deconvolution, enabling fast error estimation. We then quantify the uncertainty of the estimation, based on the available data, highlighting the areas for which priors or additional samples would be required for improved acquisition quality. We compare our approach to previous work and quantitatively evaluate our results, showing similar quality as previous work in a fraction of the time, and providing key information about the certainty of the results.

Problem statement

The reflections we observe from an object inform us about the properties of its material. Sometimes, it is difficult to know what material we are dealing with if we miss certain reflections or if a part of the object is in the shade. This can happen, for example, on a cloudy day where a glossy surface looks similar to a matte surface under certain viewing angles.

Which plane is glossy and which is matte? On the left, it's difficult to find out because of the lighting. On the right, it's immediately clear.

Two images that show the same matte and glossy surface in two lighting setups. The first image is rendered with a cloudy environment and the surfaces look similar. The second image is rendered with a sunny environment and the surfaces look very different.

Overview

The question whether we have the right lighting- and viewing conditions can be posed as a question of uncertainty. In this paper, we aim to quantify this uncertainty. Our work differs from recent contributions on uncertainty in inverse rendering by approaching the reflection equation from the signal processing framework on inverse rendering (Ramamoorthi and Hanrahan, 2001). Along the way, we find that an improved version of this framework

  • can match state-of-the-art results in a fraction of the time on the task of BRDF recovery,
  • while providing a practical way to measure uncertainty.

Relighting results

We optimize a PBR texture (base color, metallicity, roughness) on multi-view captures from Stanford ORB and relight the resulting object in Blender. More results in the supplemental material and the paper.

Uncertainty results

We show that our formulation for uncertainty using entropy matches with errors resulting from an optimization with Mitsuba.


Results showing a BRDF texture that was optimized with Mitsuba. On the right, the error is shown and a map of the uncertainty.

On the right, we show the average estimation error followed by our entropy estimation. We observe that low entropy is indicative of lower error, suggesting that it captures the sufficiency of information in the input signal. On the dice example (top row), the `one'-face is lit less than other faces and we observe highlights with lower intensity, leading to higher entropy. While we still recover the white albedo correctly, the estimation of roughness and metallicity for the dot has a high error. Similarly, the inside and lower parts of the doughnut are less observed and not lit by strong light sources. Again, entropy is high in regions of high error (especially in metallicity). The triceratops collar is down-facing and not well-lit and our entropy captures the lack of observation that leads to high error in the metallicity part.

Method

Reflection as Convolution

The signal processing framework for inverse rendering (Ramamoorthi and Hanrahan, 2001) shows that the reflection equation can be approximated as a rotational convolution of the BRDF kernel with the incoming light over the incoming- and outgoing light directions at a point on the surface. This perspective allows us to study inverse rendering in the frequency domain, here the spherical harmonics domain.

An image that shows the reflection equation as a convolution of the BRDF kernel with the incoming light over the incoming- and outgoing light directions at a point on the surface.

Robust Spherical Harmonics Transform

Our first contribution is a method to estimate the spherical harmonics coefficients for the incoming- and outgoing radiance field, for sparse and irregularly distributed viewing positions. We achieve this by a least-squares fit with a weighted L2 regularization.

An image that represents a procedure to fit spherical harmonics coefficients to an irregularly distributed, sparse set of points.

BRDF Recovery with Shadowing and Masking

Our second contribution is to use these coefficients in a BRDF optimization pipeline to estimate parameters for an analytic microfacet BRDF (Disney principled BRDF). We improve the accuracy of the convolution model by incorporating shadowing and masking.

An image that represents shadowing and masking.

Power Spectrum Approximation

Our third contribution is to develop an extremely light-weight approximation of the convolution model that operates completely in the power spectrum of the spherical harmonics. This allows us to explore hundreds of BRDF parameter combinations in a couple of milliseconds. Moreover, the power spectrum is invariant to rotations of local coordinate frame (here, rotated normals).

An image showing three plots, representing power spectra. The first plot is the power spectrum of the incoming light, the second plot of the BRDF and the third of the outgoing light. On the second plot, the graph shows alternative plots for different parameter combinations.

Uncertainty as Entropy

Our final contribution is to use statistical entropy on the likelihood of BRDF parameters to quantify uncertainty. While other methods test the likelihood function around a found optimum, our method takes a global perspective on all possible BRDF parameter combinations. This is tractable due to our power spectrum approximation.

We show three examples of power spectra for incoming and outgoing radiance, their corresponding likelihood and entropy in the adjacent figure.

An image showing three plots representing a likelihood and the corresponding entropy.

The top row shows incoming light for a dirac delta light source (constant in the spherical harmonic domain) and we see that entropy is low (H=0.25); we can be very certain about the BRDF recovery.

In the middle row, the light only has amplitude in low frequencies and many roughness values are equally likely. The higher entropy (H=0.69) is associated with higher uncertainty, which is in line with the conclusions from Ramamoorthi and Hanrahan (2001).

The bottom row shows a material with very low specular reflectance, resulting in high entropy (H=0.87) and thus high uncertainty.

Find out more

Paper Supplementary Code (to be released) arXiv

BibTeX

Coming soon